SICP 习题集 + 回答
开始学习 SICP 了!
做一个试题集来记录自己学习。
1.1 程序设计的基本元素🔗
1.1.6 条件表达式和谓词🔗
练习 1.1🔗
(位于书中第 13 页)
下面是一系列表达式,对于每个表达式,解释器将输出什么结果?假定这一系列表达式是按照给出的顺序逐个求值的。
10 ;; 10
(+ 5 3 4) ;; 12
(- 9 1) ;; 8
(/ 6 2) ;; 3
(+ (* 2 4) (- 4 6)) ;; 6
(define a 3) ;; a
(define b (+ a 1)) ;; b
(+ a b (* a b)) ;; 19
(= a b) ;; #f
(if (and > b a) (< b (* a b)))
b
a) ;; 4
(cond ((= a 4) 6)
((= b 4) (+ 6 7 a))
(else 25)) ;; 16
(+ 2 (if (> b a) b a)) ;; 6
(* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1)) ;; 16
练习 1.2🔗
(位于书中第 13 页)
请将下面表达式变换为前缀形式:
$$ \frac{5+4+(2-(3-(6+\frac{4}{5})))}{3(6-2)(2-7)} $$
(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5)))))
(* 3 (- 6 2) (- 2 7)))
练习 1.3🔗
(位于书中第 13 页)
请定义一个过程,它以三个数为参数,返回其中较大的两个数之和。
(define (sum-of-two-biggies a b c)
(define (bigger x y) (if (> x y) x y))
(define (smaller x y) (if (> x y) y x))
(+ (bigger a b)
(bigger (smaller a b) c)))
练习 1.4🔗
(位于书中第 13 页)
请仔细考察上面给出的允许运算符为复合表达式的组合式的求值模型,根据对这一模型的认识描述下面的行为:
(define (a-plus-abs-b a b)
((if (> b 0) + -) a b))
定义一个函数 a-plus-abs-b;对于参数 a 和 b,如果 b > 0,返回 a + b,否则返回 a - b。
测试:
(a-plus-abs-b 2 -3) ;; 5
(a-plus-abs-b 2 2) ;; 4
练习 1.5🔗
(位于书中第 13 页)
Ben Bitdiddle 发明了一种检测方法,能够确定解释器究竟采用哪种序求值,是采用应用序,还是采用正则序。它定义了下面两个过程。
(define (p) (p))
(define (test x y)
(if (= x 0)
0
y))
然后他求值下面的表达式:
(test 0 (p))
如果某个解释器采用的是应用序求值,Ben 会看到什么样的情况?如果解释器采用正则序求值,他又会看到什么情况?请对你的对回答做出解释。(无论采用正则序或者应用序,假定特殊形式 if 的求值规则总是一样的。其中谓词部分先行求值,根据其结果确定随后求值的子表达式部分。)
如果采用的是应用序求值,程序会陷入死循环,因为应用序在调用函数时求值,在执行 (test 0 (p)) 时,函数 p 会被立即执行,然后进入死循环。
如果采用正则序求值,这会输出 0,因为正则序的解释器会先将函数 (test 0 (p)) 展开成 (if (= 0 0) 0 (p));然后根据特殊形式 if 的求值规则,谓词部分先被执行,结果为 #t;然后直接返回 0,函数 p 不会被执行。
1.1.7 实例:采用牛顿法求平方根🔗
练习 1.6🔗
(位于书中第 16 页)
Alyssa P. Hacker 看不出为什么需要将 if 提供为一种特殊形式,她问:“为什么我不能直接通过 cond 将它定义为一个常规过程呢?” Alyssa 的朋友 Eva Lu Ator 断言确实可以这样做,并定义了一个 if 的新版本:
(define (new-if predicate then-clause else-clause)
(cond (predicate then-clause)
(else else-clause)))
Eva 给 Alyssa 演示她的程序:
(new-if (= 2 3) 0 5) ;; 5
(new-if (= 1 1) 0 5) ;; 0
她很高兴地用自己的 new-if 重写了求平方根的程序:
(define (sqrt-item guess x)
(new-if (good-enough? guess x)
guess
(sqrt-item (improve guess x) x)))
当 Alyssa 试着用这个过程去计算平方根时会发生什么事件呢?请给出解释。
会因为递归层数太深,超过了最大的递归深度而强制退出。
在特殊形式 if 中 (我们假定特殊形式 if 的函数签名为 (define (if (predicate then-clause else-clause)) (...))),程序会根据 predicate 的结果来决定执行 then-clause 或是 else-clause。但在 new-if 中,由于 new-if 是普通函数,所以无论 predicate 的结果如何,then-clause 和 else-clause 都会被执行,于是就轻松点超过了最大递归深度而被强制退出了。
练习 1.7🔗
(位于书中第 16 页)
对于确定很小的数的平方根而言,在计算平方根中使用的检测 good-enough? 是很不好的。还有,在现实的计算机里,算术运算总是以一定的有限精度进行的。这也会使我们的检测不适合非常大的数的计算。请解释上述论断,用例子说明对很小和很大的数,这种检测都可能失败。实现 good-enough? 的另一种策略是监视猜测值在从一次选代到下一次的变化情况,当改变值相对于猜测值的比率很小时就结束。请设计一个采用这种终止测试方式的平方根过程。对于很大和很小的数,这一方式都能工作吗?
由于我使用的是猜测值的平方与计算值的差小于 0.01 作为判断成功的条件。但测试值很小时,以 0.01 作为判断目标所产生的误差就会很大。例如:
(sqrt 0.00009) ;; 得到 0.06297740362374088;正确值应当是 0.007745968689668512
而对于很大的值,由于 Scheme 的小数精度是有限的,如果两数的差值超过了 Scheme 的小树精度,程序会陷入死循环。
(sqrt 8935827881491184718748172411241129912848) ;; 死循环
对于监视猜测值在从一次选代到下一次的变化情况,当改变值相对于猜测值的比率很小时就结束这种终止策略的实现:
(define (good-enough? old new)
(> 0.01 (/ (abs (- new old)) old)))
(define (sqrt-item guess x)
(define new-guess (improve guess x))
(if (good-enough? guess new-guess)
new-guess
(sqrt-item new-guess x)))
对于很大和很小的数,这一方式也能很好的工作!
(sqrt 0.00009) ;; 0.009486833049684392
(writeln (sqrt 8935827881491184718748172411241129912848)) ;; 9.453022025155877e+19
练习 1.8🔗
(位于书中第 17 页)
求立方根的牛顿法基于如下事实,如果 $y$ 是 $x$ 的立方根的一个近似值,那么下式将给出一个更好的近似值:
$$ \frac{x/y^{2} + 2y}{3} $$
请利用这一公式实现一个类似平方根过程的求立方根的过程。
(define (good-enough? old new)
(> 0.01 (/ (abs (- new old)) old)))
(define (sqrt3-item guess x)
(define new-guess (better-guess guess x))
(if (good-enough? guess new-guess)
new-guess
(sqrt3-item new-guess x)))
(define (better-guess y x)
(/ (+ (/ x (square y)) (* 2 y)) 3))
(define (sqrt3 x)
(sqrt3-item 1.0 x))
测试:
(sqrt3 1000) ;; 10.000000145265767
(sqrt3 371289471892) ;; 7187.3964104921715
1.2 过程与它们所产生的计算🔗
1.2.1 线性的递归和迭代🔗
练习 1.9🔗
(位于书中第 23 页)
下面几个过程各定义了一种加起两个正整数的方法,它们都基于过程 inc (它将参数增加1) 和 dec (它将参数减少1)。
(define (+ a b)
(if (= a 0)
b
(inc (+ (dec a) c))))
(define (+ a b)
(if (= a 0)
b
(+ (dec a) (inc b))))
请用代换模型展示这两个过程在求值 (+ 4 5) 时所产生的计算过程。这些计算过程是递归的或者选代的吗?
对于方法一,有如下代换模型:
(+ 4 5)
(inc (+ 3 5))
(inc (inc (+ 2 5))
(inc (inc (inc (+ 1 5))))
(inc (inc (inc (+ 0 5))))
(inc (inc (inc (inc 5))))
(inc (inc (inc 6)))
(inc (inc 7))
(inc 8)
9
这种方法是线性递归的。
对于方法二,有如下代换模型:
(+ 4 5)
(+ 3 6)
(+ 2 7)
(+ 1 8)
(+ 0 9)
9
这种方法是线性迭代的。
练习 1.10🔗
(位于书中第 24 页)
下面过程计算一个成为 Ackermann 函数的数学函数:
(define (A x y)
(cond ((= y 0) 0)
((= x 0) (* 2 y))
((= y 1) 2)
(else (A (- x 1)
(A x (- y 1))))))
下面各表达式的值是什么:
(A 1 10)
(A 2 4)
(A 3 3)
请考虑下面的过程,其中的 A 就是上面定义的过程:
(define (f n) (A 0 n))
(define (g n) (A 1 n))
(define (h n) (A 2 n))
(define (k n) (* 5 n n))
请给出过程 f、g 和 h 对给定整数值 n 所计算的函数的数学定义。(例如,(k n) 计算的是 $5n^{2}$)
(A 1 10) ;; 1024
(A 2 4) ;; 65536
(A 3 3) ;; 65536
我们将 (f n) 通过代换模型的方法展开:
(f n)
(A 0 n)
(* 2 n)
我们可以得出过程 f 对给定整数值 n 所计算的函数的数学定义为:$ f(n)=2n $
将 (g n) 通过代换模型的方法展开:
(g n)
(A 1 n)
(A 0 (A 1 (- n 1)))
(A 0 (A 0 (A 1 (- (- n 1) 1))))
...
通过观察我们可以得出:$ g(n)=2^n $
根据 $f(n)$ 和 $g(n)$,我们推测 $ h(n)=2^{2^{\ldotp^{\ldotp^{\ldotp^2}}}} $
将整数带入进行验算:
| $n$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $\dots$ |
|---|---|---|---|---|---|---|---|
| $h(n)$ | $0$ | $2$ | $4$ | $16$ | $65536$ | $200\dots6736$ | $\dots$ |
基本可以验证我们的推测。
1.2.2 树形递归🔗
练习 1.11🔗
(位于书中第 27 页)
函数 $f$ 由如下的规则定义:如果 $ n<3 $,那么 $ f(n)=n $;如果 $ n\geq3 $,那么 $ f(n)=f(n-1)+2f(n-2)+3f(n-3) $。请写一个采用递归计算过程计算 $f$ 的过程。再写一个采用迭代计算过程计算 $f$ 的过程。
采用递归计算过程计算 $f$:
(define (f n)
(if (>= n 3)
(+ (f (- n 1)) (* 2 (f (- n 2))) (* 3 (f (- n 3))))
n))
验证:
| $n$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $\dots$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $f(n)$ | $0$ | $1$ | $2$ | $4$ | $11$ | $25$ | $59$ | $142$ | $335$ | $796$ | $\dots$ |
至于通过迭代计算过程计算 $f$,我们先将一些简单的大于等于 $3$ 的整数代入到 $f$:
$$ f(3) = f(2) + 2f(1) + f(0) \newline f(4) = f(3) + 2f(2) + f(1) \newline f(5) = f(4) + 2f(3) + f(2) \newline\dots $$
通过观察,我们发现存在着某种“错位”:
- $f(3)$ 位于 $f(4)$ 的“一号位置”和 $f(5)$ 的“二号位置”
- $f(4)$ 位于 $f(5)$ 的“一号位置”
- …
f(3)
f(4) \ f(3)
f(5) \ f(4) \ f(3)
...
通过进一步归纳,我们得到了一个 $f$ 的变形式:
$$ f(i+3) = f(i+2) + 2f(i+1) + 3f(i) \pod{i = 1,2,3,\dots,n-3; n\geq3}$$
根据变形后的 $f$,我们令参数 a、b、c、i 分别表示 $f(i+2)$、$f(i+1)$、$f(i)$、$i$。
然后从 $f(0)$ 开始,一步步计算出 $f(n)$:
(define (f n)
(define (f-iter a b c i)
(if (= n i)
c
(f-iter (+ a (* 2 b) (* 3 c)) ;; new a
a ;; new b
b ;; new c
(+ i 1))))
(f-iter 2 1 0 0))
验证:
| $n$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $\dots$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $f(n)$ | $0$ | $1$ | $2$ | $4$ | $11$ | $25$ | $59$ | $142$ | $335$ | $796$ | $\dots$ |
练习 1.12🔗
(位于书中第 27 页)
下面数值模式称为帕斯卡三角形:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
三角形的边界上的数值都是 $1$,内部的每个数是位于它上面的两个数之和。请写一个过程,它采用递归计算过程计算出帕斯卡三角形的各个元素。
通过递归实现,
算法:
$$ \dbinom{row}{col}=\dbinom{row-1}{col-1}+\dbinom{row-1}{col} $$
代码:
(define (pascal row col)
(cond ((> col row) 0)
((or (= col 0) (= row col)) 1)
(else (+ (pascal (- row 1) (- col 1))
(pascal (- row 1) col)))))
通过迭代实现,
算法:
$$ \dbinom{row}{col}=\frac{row!}{col!(row-col)!} $$
代码:
(define (factorial x)
(define (factorial-item acc item)
(if (> item 0)
(factorial-item (* item acc) (- item 1))
acc))
(factorial-item 1 x))
(define (pascal row col)
(if (or (> col row) (< row 0) (< col 0))
0
(/ (factorial row) (* (factorial col) (factorial (- row col))))))
练习 1.13🔗
(位于书中第 28 页)
证明 $Fib(n)$ 是最接近 $ \frac{\varphi^n}{\sqrt{5}} $ 的整数,其中 $ \varphi=\frac{1+\sqrt{5}}{2} $。提示:利用归纳法和斐波那契数列的定义,证明 $ Fib(n)=\frac{\varphi^n-\gamma^n}{\sqrt{5}} $。
设 $ Fib(n)=\frac{\varphi^n-\gamma^n}{\sqrt{5}} $,
则
$ Fib(n+1) = \frac{\varphi^{n+1}-\gamma^{n+1}}{\sqrt{5}} = \frac{\varphi^n\varphi-\gamma^n\gamma}{\sqrt{5}} = \frac{\varphi^n\frac{1+\sqrt{5}}{2}-\gamma^n\frac{1-\sqrt{5}}{2}}{\sqrt{5}} \newline = \frac{1}{2}(\frac{\varphi^n-\gamma^n}{\sqrt{5}}+\frac{\sqrt{5}(\varphi^n+\gamma^n)}{\sqrt{5}}) = \frac{1}{2}Fib(n)\frac{\varphi^n+\gamma^n}{2}, $
$ Fib(n+2) = \frac{\varphi^{n+2}-\gamma^{n+2}}{\sqrt{5}} = \frac{\varphi^n\varphi^2-\gamma^n\gamma^2}{\sqrt{5}} = \frac{\varphi^n(\frac{1+\sqrt{5}}{2})^2-\gamma^n(\frac{1-\sqrt{5}}{2})^2}{\sqrt{5}} \newline = \frac{1}{2}(\frac{3(\varphi^n-\gamma^n)}{\sqrt{5}}+\frac{\sqrt{5}(\varphi^n+\gamma^n)}{\sqrt{5}}) = \frac{3}{2}Fib(n)\frac{\varphi^n+\gamma^n}{2}; $
可证 $ Fib(n+2) = Fib(n+1)+Fib(n) $;
又
$ \frac{\varphi^0-\gamma^0}{\sqrt{5}} = 0 = Fib(0), $
$ \frac{\varphi^1-\gamma^1}{\sqrt{5}} = 1 = Fib(1); $
由此可知 $ Fib(n) = \frac{\varphi^n-\gamma^n}{\sqrt{5}} $ 成立。
由于 $Fib(n)$ 可以拆成两数之差的形式:$ Fib(n)=\frac{\varphi^n-\gamma^n}{\sqrt{5}}=\frac{\varphi^n}{\sqrt{5}}-\frac{\gamma^n}{\sqrt{5}} $
而 $ \frac{1}{\sqrt{5}} < \frac{1}{2}, \lvert \gamma \rvert = \lvert \frac{1-\sqrt{5}}{2} \rvert < 1 $
故 $ \lvert \frac{\gamma^n}{\sqrt{5}} \rvert < \frac{1}{2} $
即 $ \lvert Fib(n)-\frac{\varphi^n}{\sqrt{5}} \rvert < \frac{1}{2} $
故得证:$ Fib(n) $ 是与 $ \frac{\varphi^n}{\sqrt{5}} $ 最接近的整数
1.2.3 增长的阶🔗
练习 1.14🔗
(位于书中第 29 页)
请画出有关的树,展示 1.2.2 节的过程 count-change 在将 11 美分换成硬币时所产生的计算过程。相对于被换现金量的增加,这一计算过程的空间和步数增长的阶各是什么?
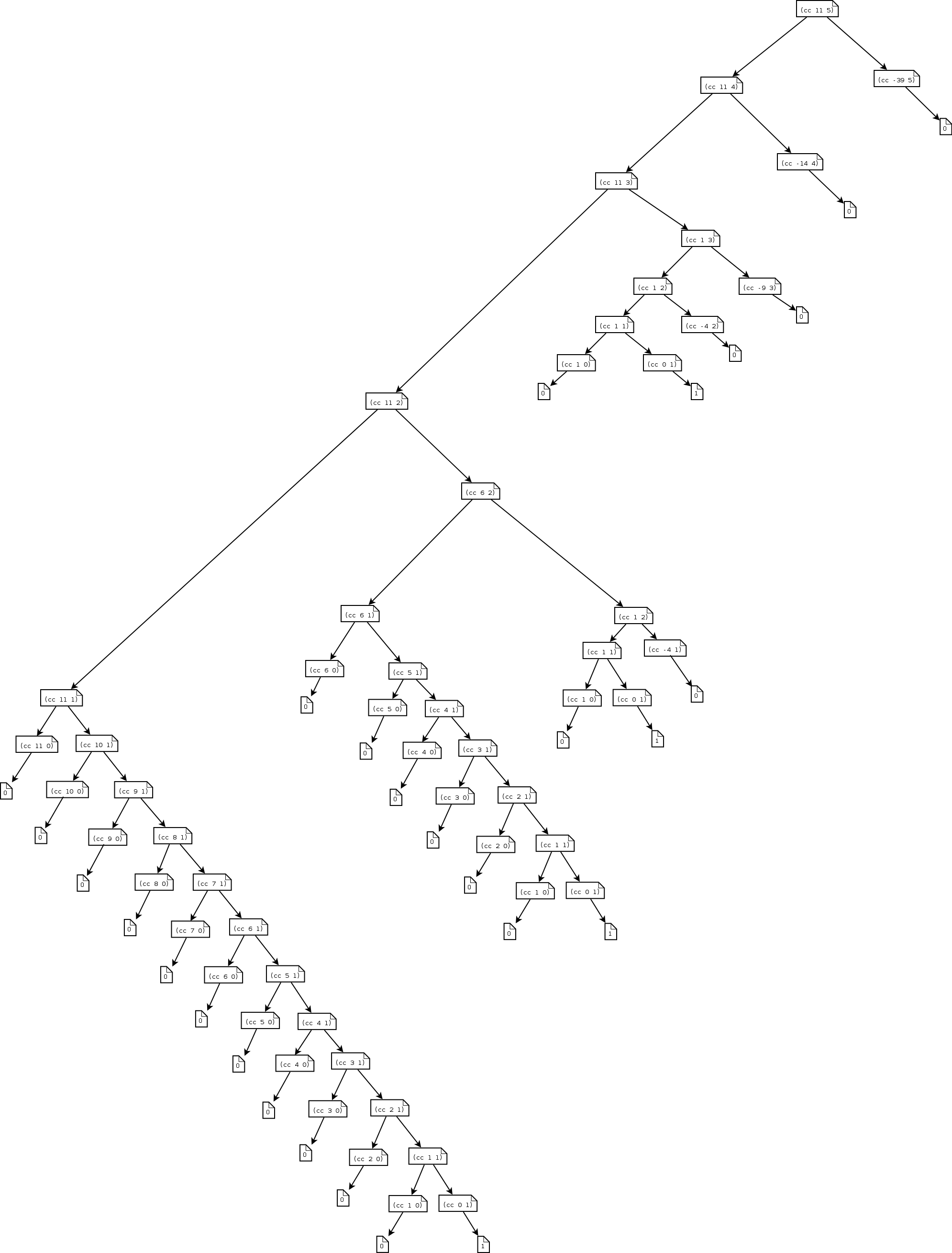
练习1.15🔗
(位于书中第 29 页)
在角 (用弧度描述) $x$ 足够小时,其正弦值可以用 $\sin{x} \approx x$ 算,而三角恒等式:
$$ \sin{x} = 3\sin{\frac{x}{3}}-4\sin^{3}{\frac{x}{3}} $$
可以减小 $\sin$ 的参数的大小 (为完成这一练习,我们认为一个角是“足够小”,如果其数值不大于 $0.1$ 弧度)。这些想法都体现在下达过程中:
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
a) 在求值 (sine 12.15) 时,p 将被使用多少次?
答:p 一共运行了 5 次。
b) 在求值 (sine a) 时,由过程 sine 所产生的计算过程使用的空间和步数 (作为 a 的函数) 增长的阶是什么?
答:在求值 (sine a) 的时候,a 每次都被除以 3.0 ,而 sine 是一个递归程序,因此它的时间和空间复杂度都是 $O(\log{a})$。
1.2.4 求幂🔗
练习 1.16🔗
(位于书中第 30 页)
请定义一个过程,它能产生出一个按照迭代方式的求幂计算过程,其中使用一系列的求平方,就像一样 fast-expt 只用对数个步骤那样。(提示:请利用关系 $(b^{n/2})^2=(b^2)^{n/2}$,除了指数 n 和基数 b 之外,还应维持一个附加的状态变量 a,并定义好状态变换,使得从一个状态转到另一状态时乘积 $a b^n$不变。在计算过程开始时令 a 取值 1,并用计算过程结束时 a 的值作为回答。一般说,定义一个不变量,要求它在状态之间保持不变,这一技术是思考迭代算法设计问题时的一种非常强有力的方法。)
(define (square x) (* x x))
(define (even? x) (= (remainder x 2) 0))
(define (fast-expt b n)
(define (fast-expt-item acc m)
(cond ((= m 0) acc)
((= m 2) (* acc (square b)))
((even? m) (fast-expt-item (* acc (square b)) (/ m 2)))
(else (fast-expt-item (* acc b) (- m 1)))))
(fast-expt-item 1 n))
练习 1.17🔗
(位于书中第 31 页)
本节里的求幂算法的基础就是通过反复做乘法去求乘昇。与此类似,也可以通过反复做加法的方式求出乘积。下面的乘积过程与 expt 过程类似 (其中假定我们的语言只有加法而没有乘法):
(define (* a b)
(if (= b 0)
0
(+ (* a (- b 1)))))
这一算法具有相对于 b 的线性步数。现在假定除了加法之外还有运算 double,它能求出一个整数的两倍;还有 halve,它将一个 (偶数) 除以 2。请用这些运算设计一个类似 fast-expt 的求乘积过程,使之只用对数的计算步数。
(define (even? x) (= (remainder x 2) 0))
(define (double x) (+ x x))
(define (halve x) (/ x 2))
(define (multi a b)
(cond ((= b 0) 0)
((= b 2) (double a))
((even? b) (+ (double a) (multi a (halve b))))
(else (+ a (multi a (- b 1))))))
练习 1.18🔗
(位于书中第 31 页)
利用练习 1.16和 练习 1.17 的结果设计一个过程,它能产生出一个基于加、加倍和折半运算的选代计算过程,只用对数的步数就能求出两个整数的乘积。
(define (double x) (+ x x))
(define (halve x) (/ x 2))
(define (even? x) (= (remainder x 2) 0))
(define (multi a b)
(define (multi-item acc n)
(cond ((= n 0) acc)
((= n 2) (+ acc (double a)))
((even? n) (multi-item (+ acc (double a)) (halve n)))
(else (multi-item (+ acc a) (- n 1)))))
(multi-item 0 b))
练习 1.19🔗
(位于书中第 31 页)
存在着一种以对数步数求出斐波那契数的巧妙算法。请回忆 1.2.2 节 fib-iter 计算过程中状态变量 a 和 b 的变换规则,$a \larr a+b$ 和 $b \larr a$,现在将这种变换称为 $T$ 变换。通过观察可以发现,从 1 和 0 开始将 $T$ 反复应用 n 次,将产生出一对数 $Fib(n+1)$ 和 $Fib(n)$。换句话说,斐波那契数可以通过将 $T^n$ (变换 $T$ 的 n 次方) 应用于对偶 $(1,0)$ 而产生出来。现在将 $T$ 看作变换族 $T_{pq}$ 中 $p=0$ 且 $q=1$ 的特殊情况,其中 $T_{pq}$ 是对于对偶 $(a, b)$ 按照 $a \larr a+b$ 和 $b \larr a$ 规则的变换。请证明,如果我们应用变换 $T_{pq}$ 两次,其效果等同于应用同样形式的一次变换 $T_{p^{′}q^{′}}$,其中的 $p^{′}$ 和 $q^{′}$ 可以由 $p$ 和 $q$ 算出来。这就指明了一条求出这种变换的平方的路径,使我们可以通过连续求平方的方式去计算 $T^{n}$,就像 fast-expt 过程里所做的那样。将所有这些集中到一起,就形成了下面的过程,其运行只需要对数的步数:
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(fib-iter a
b
<??> ; compute p′
<??> ; compute q′
(/ count 2)))
(else (fib-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- count 1)))))
已知对于对偶 $(a, b)$,有变换 $T_{pq}$ 为 $a \larr bq+a(p+q)$ 和 $b \larr bp+a$。
那么对于 $T_{pq}$ 的平方 $(T_{pq})^{2}$ 来说,有变换
$ a \larr (bp+aq)q+(bq+a(p+q))(p+q)=b(2pq+q^{2})+a(p^{2}+q^{2}+2pq+q^{2}) \newline b \larr (bp+aq)p+(bq+a(p+q))q=b(p^{2}+q^{2})+a(2pq+q^{2}) $
通过对比 $T_{pq}$ 和 $(T_{pq})^{2}$,可以得出变换 $T_{p^{′}q^{′}}$,其中 $p^{′}=p^{2}+q^{2}$,且 $q^{′}=2pq+q^{2}$。
因此,每次当 $N$ 为偶数时,我们可以通过应用变换 $T_{p^{′}q^{′}}$ 来减少一半计算 $T^{N}$ 所需的计算量,从而得出对数复杂度的斐波那契计算函数:
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(fib-iter a
b
(+ (square p) (square q))
(+ (* 2 p q) (square q))
(/ count 2)))
(else (fib-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- count 1)))))
(to be continue…)